Correct reasoning is the basis for all sound thought!
THE AXIOMS OF DIALECTIC AND OF
SYLLOGISM.
There are certain principles known as the Laws of Thought or the Maxims of Consistency. They are variously expressed, variously demonstrated, and variously interpreted, but in one form or another they are often said to be the foundation of all Logic. It is even said that all the doctrines of Deductive or Syllogistic Logic may be educed from them. Let us take the most abstract expression of them, and see how they originated. Three laws are commonly given, named respectively the Law of Identity, the Law of Contradiction and the Law of Excluded Middle.
1. The Law of Identity. A is A. Socrates is Socrates. Guilt is guilt.
2. The Law of Contradiction. A is not not-A. Socrates is not other than Socrates. Guilt is not other than guilt. Or A is not at once b and not-6. Socrates is not at once good and not-good. Guilt is not at once punishable and not-punishable.
3. The Law of Excluded Middle. Everything is either A or not-A; or, A is either b or not-£. A given thing is either Socrates or not-Socrates, either guilty or not-guilty. It must be one or the other: no middle is possible.
The Figures of the Syllogism
As described by Petrus Hispanius.
The vowels indicate the type of statements:
I Barbara all M is P; all S is M: all S is P I Celarent no M is P; all S is M: no S is P I Darii all M is P; some S is M: some S is P I Ferio no M is P; some S is M: some S is not P II Cesare no P is M; all S is M: no S is P II Camestres all P is m; no S is M: no S is P II Festino no P is M; some S is M: some S is not P II Baroko
Fakofoall P is M; some s is not M: some S is not P III Darapti all M is P; all M is S: some S is P III Disamis some M is P; all M is S: some S is P III Datisi all M is P; some M is S: some S is P III Felapton no M is P; all M is S: some S is not P III Bocardo
Dokamoksome M is not P; all M is S: some S is not P III Ferison no M is P: some M is S: some S is not P IV Bramantip all P is M; all M is S: some S is P IV Camenes all P is M; no M is S: no S is P IV Dimaris some P is M; all M is S: some S is P IV Fesapo no P is M; all M is S: some S is not P IV Fresison no P is M; some M is S: some S is not P
A - Universal affirmative
E - Universal negative
I - Particular affirmative
O - Particular negative
Conversions of II, III, IV to corresponding I:
S - simple
P - per accidens
M - transpose premises
N - reductio ad absurdum
Daniel Seely Gregory's "Practical logic: or, The art of thinking" (1881) says: "The initial consonant, B, C, D or F, in the last three Figures indicates the mood in the first Figure to which the syllogism reduces. Thus, a syllogism in the mood Cesare, reduces to Celarent. The inserted consonants, s, p, k, f, m, indicate the various processes in reduction. S indicates that the proposition symbolized by the vowel preceding it is to be converted simply; p, by limitation or per aociden; k, by contraposition; f, by infinitation or obversion. The letter m (mutari) indicates that the premises of the preceding judgment are to be transposed. The p in Bramantip shows that, after converting simply, the premises warrant a universal conclusion. The other consonants, b, d, l, n, r, t, are not significant, but are inserted for the sake of euphony, or of the metre in the mnemonic hexameters invented, to keep the moods and figures in mind, by Petrus Hispanus, who died in 1277 as Pope John XXII."
The Traditional Square of Opposition
First published Fri Aug 8, 1997; substantive revision Tue Aug 21, 2012This entry traces the historical development of the Square of Opposition, a collection of logical relationships traditionally embodied in a square diagram. This body of doctrine provided a foundation for work in logic for over two millenia.
The doctrine of the square of opposition originated with Aristotle in the fourth century BC and has occurred in logic texts ever since. Although severely criticized in recent decades, it is still regularly referred to. The point of this entry is to trace its history from the vantage point of the early twenty-first century, along with closely related doctrines bearing on empty terms.
The square of opposition is a group of theses embodied in a diagram. The diagram is not essential to the theses; it is just a useful way to keep them straight. The theses concern logical relations among four logical forms:
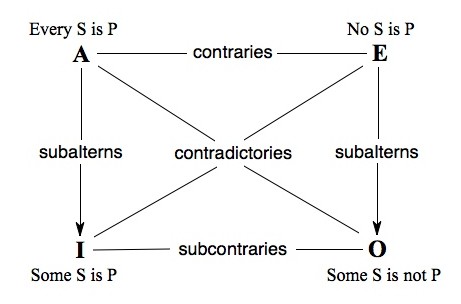
The diagram for the traditional square of opposition is:
NAME FORM TITLE A Every S is P Universal Affirmative E No S is P Universal Negative I Some S is P Particular Affirmative O Some S is not P Particular Negative
The theses embodied in this diagram I call ‘SQUARE’. They are:
SQUARE
- ‘Every S is P’ and ‘Some S is not P’ are contradictories.
- ‘No S is P’ and ‘Some S is P’ are contradictories.
- ‘Every S is P’ and ‘No S is P’ are contraries.
- ‘Some S is P’ and ‘Some S is not P’ are subcontraries.
- ‘Some S is P’ is a subaltern of ‘Every S is P’.
These theses were supplemented with the following explanations:
- ‘Some S is not P’ is a subaltern of ‘No S is P’.
- Two propositions are contradictory iff they cannot both be true and they cannot both be false.
- Two propositions are contraries iff they cannot both be true but can both be false.
- Two propositions are subcontraries iff they cannot both be false but can both be true.
Probably nobody before the twentieth century ever held exactly these views without holding certain closely linked ones as well. The most common closely linked view that is associated with the traditional diagram is that the E and I propositions convert simply; that is, ‘No S is P’ is equivalent in truth value to ‘No P is S’, and ‘Some S is P’ is equivalent in truth value to ‘Some P is S’. The traditional doctrine supplemented with simple conversion is a very natural view to discuss. It is Aristotle's view, and it was widely endorsed (or at least not challenged) before the late 19th century. I call this total body of doctrine ‘[SQUARE]’:
- A proposition is a subaltern of another iff it must be true if its superaltern is true, and the superaltern must be false if the subaltern is false.
[SQUARE] =df SQUARE + “the E and I forms convert simply”where
A proposition converts simply iff it is necessarily equivalent in truth value to the proposition you get by interchanging its terms.So [SQUARE] includes the relations illustrated in the diagram plus the view that ‘No S is P’ is equivalent to ‘No P is S’, and the view that ‘Some S is P’ is equivalent to ‘Some P is S’.
Excellent way of telling, and good article to get facts about my presentation focus,
ReplyDeletewhich i am going to deliver in university.
whoah this blog is wonderful i love studying your articles.
ReplyDeleteKeep up the good work! You know, many individuals
are hunting around for this info, you could aid them greatly.